Electromagnetomechanics
Introduction
This section for electromagnetomechanics splits into magnetomechanics and electromechanics. Magnetomechanics deals with the steady-state force created by a magnetic field, which usually results from a permanent magnet or a constant current flowing through a conductor, and the mechanical responses caused by this magnetostatic (or magnetic) force. For electromechanics, two major electromechanical mechanisms, i.e., piezoelectric effect and piezoresistive effect, will be discussed for their mathematical formulations and applications.
$\space$Mathematical Formulation
Piezoelectricity as a reversible process requires a fully coupled constitutive relationship that combines the constitutive relationships in both the electric field and mechanical field. For the electric field, we have the following relationship between the electric displacement field $D$ and the electric field $E$:
\[D=\varepsilon E.\]For the mechanical field, we can recall Hooke's Law for linearly elastic materials:
\[S=sT,\]where $S$ is the strain, $s$ is the compliance and $T$ is the stress. Here symbols for the mechanical field are different from the common ones, i.e., those in the other places of this website, due to the conflicts in the choice of symbols in the studies of the mechanical field and electric field.
To couple the two fields, one more material property, which is formulated as a matrix, needs to be added to describe the couplings between the two fields. This type of strong coupling, which is formulated using the following equations, is similar to that in poroelasticity,
\[S=sT+d^{{\rm T}} E\] \[D=dT+\varepsilon E.\]By employing the Voigt notation, we can obtain the following formulations for typical piezomaterials such as tetragonal PZT and BaTiO${}_{3}$:
\[\left[\begin{array}{c} {S_{1} } \\ {S_{2} } \\ {S_{3} } \\ {S_{4} } \\ {S_{5} } \\ {S_{6} } \end{array}\right]=\left[\begin{array}{cccccc} {s_{11} } & {s_{12} } & {s_{13} } & {0} & {0} & {0} \\ {s_{21} } & {s_{22} } & {s_{23} } & {0} & {0} & {0} \\ {s_{31} } & {s_{32} } & {s_{33} } & {0} & {0} & {0} \\ {0} & {0} & {0} & {s_{44} } & {0} & {0} \\ {0} & {0} & {0} & {0} & {s_{55} } & {0} \\ {0} & {0} & {0} & {0} & {0} & {s_{66} } \end{array}\right]\left[\begin{array}{c} {T_{1} } \\ {T_{2} } \\ {T_{3} } \\ {T_{4} } \\ {T_{5} } \\ {T_{6} } \end{array}\right]+\left[\begin{array}{ccc} {0} & {0} & {d_{31} } \\ {0} & {0} & {d_{32} } \\ {0} & {0} & {d_{33} } \\ {0} & {d_{24} } & {0} \\ {d_{15} } & {0} & {0} \\ {0} & {0} & {0} \end{array}\right]\left[\begin{array}{c} {E_{1} } \\ {E_{2} } \\ {E_{3} } \end{array}\right]\] \[\left[\begin{array}{c} {D_{1} } \\ {D_{2} } \\ {D_{3} } \end{array}\right]=\left[\begin{array}{cccccc} {0} & {0} & {0} & {0} & {d_{15} } & {0} \\ {0} & {0} & {0} & {d_{24} } & {0} & {0} \\ {d_{31} } & {d_{32} } & {d_{33} } & {0} & {0} & {0} \end{array}\right]\left[\begin{array}{c} {T_{1} } \\ {T_{2} } \\ {T_{3} } \\ {T_{4} } \\ {T_{5} } \\ {T_{6} } \end{array}\right]+\left[\begin{array}{ccc} {\varepsilon _{11} } & {0} & {0} \\ {0} & {\varepsilon _{22} } & {0} \\ {0} & {0} & {\varepsilon _{33} } \end{array}\right]\left[\begin{array}{c} {E_{1} } \\ {E_{2} } \\ {E_{3} } \end{array}\right]\]where the first equation represents the relationship for the converse piezoelectric effect (coupling from the electric field to the mechanical field) and the latter for the direct piezoelectric effect (coupling from the mechanical field to the electric field).
The piezoelectric coefficients, i.e., $d_{ij} $ can be determined as follows \[d_{ij} =\left. \left(\frac{\partial D_{i} }{\partial T_{j} } \right)\right|_{E=0} =\left. \left(\frac{\partial S_{j} }{\partial E_{i} } \right)\right|_{T=0} .\]The mathematical formulations for other piezoelectric materials will be different, depending on the specific coupling mechanisms determined by the crystal structures.
$\space$Piezoresistive
The piezoresistive effect is the change in the electrical resistivity of a semiconductor or a metal due to mechanical strains.
In electrically conductive and semi-conductive materials, strains can change the inter-atomic spacing and consequently the easiness for electrons to be raised into the conduction band. This leads to a change in the resistivity of the material. A linear relationship usually can be assumed between the resistivity and the strain within a certain range of strains. This proportionality is the piezoresistive coefficient and can be mathematically defined as \[\rho _{\sigma } =\frac{\left(\frac{\partial \rho }{\rho } \right)}{\varepsilon } ,\] where, $\rho _{\sigma } $ is the piezoresistive coefficient, $\partial \rho $ is the change in the resistivity, $\rho $is the original resistivity, and $\varepsilon $ is the strain.
$\space$Example
The plate is made of transversely isotropic PZT material. The transverse plane of the material (direction 1 & 2 or x & y) coincides with the plane of the plate. The constitutive relationships of the material are as follows:
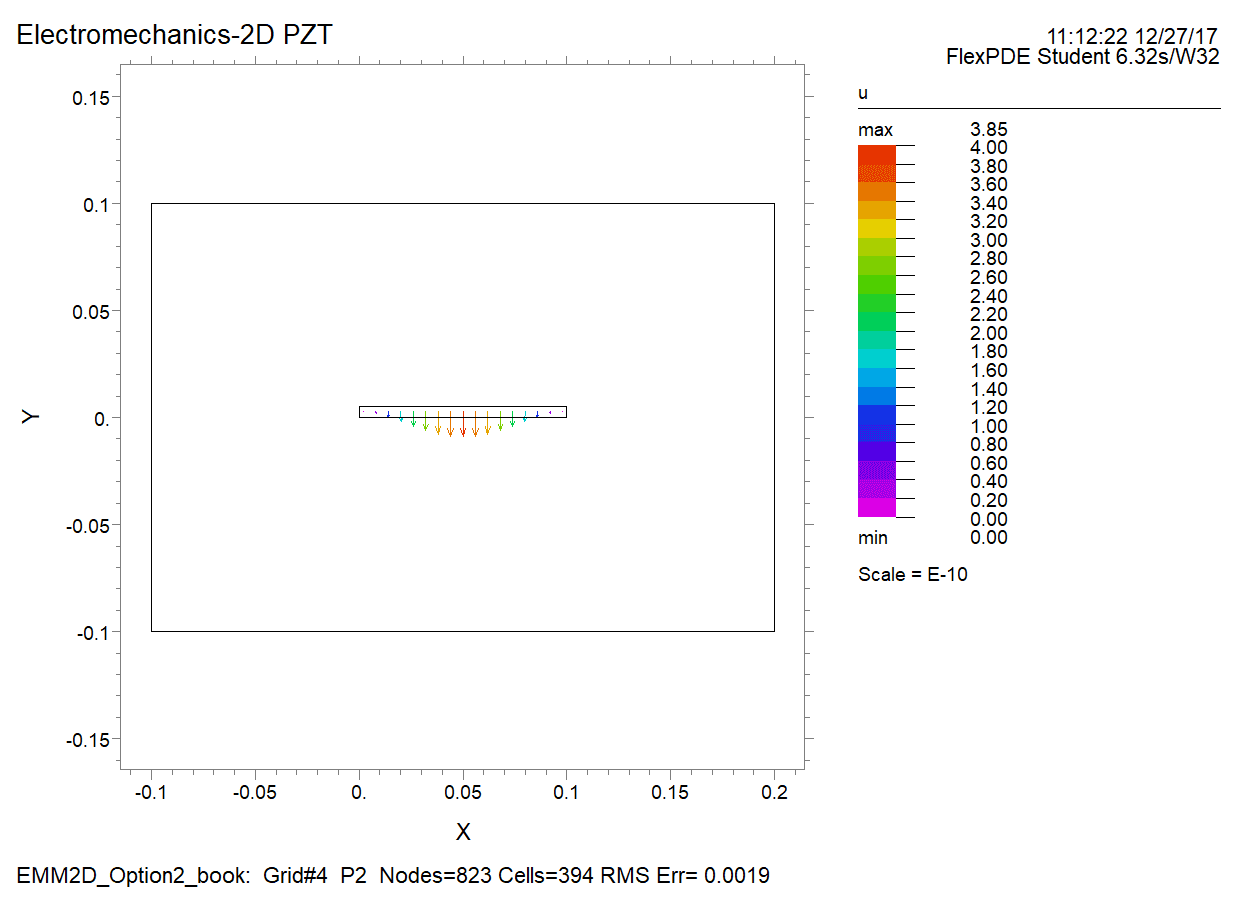
\[\left[\begin{array}{c} {S_{1} } \\ {S_{2} } \\ {S_{3} } \\ {S_{4} } \\ {S_{5} } \\ {S_{6} } \end{array}\right]=\left[\begin{array}{cccccc} {139} & {77.8} & {74.3} & {0} & {0} & {0} \\ {77.8} & {139} & {74.3} & {0} & {0} & {0} \\ {74.3} & {74.3} & {115} & {0} & {0} & {0} \\ {0} & {0} & {0} & {\frac{139-77.8}{2} } & {0} & {0} \\ {0} & {0} & {0} & {0} & {25.6} & {0} \\ {0} & {0} & {0} & {0} & {0} & {25.6} \end{array}\right]{\rm GPa}\otimes \] \[\left[\begin{array}{c} {T_{1} } \\ {T_{2} } \\ {T_{3} } \\ {T_{4} } \\ {T_{5} } \\ {T_{6} } \end{array}\right]+\left[\begin{array}{ccc} {0} & {0} & {-5.2} \\ {0} & {0} & {-5.2} \\ {0} & {0} & {15.1} \\ {0} & {12.7} & {0} \\ {12.7} & {0} & {0} \\ {0} & {0} & {0} \end{array}\right] \frac{{\rm C}}{{\rm m}^{{\rm 2}} } \otimes \left[\begin{array}{c} {E_{1} } \\ {E_{2} } \\ {E_{3} } \end{array}\right]\] \[\left[\begin{array}{c} {D_{1} } \\ {D_{2} } \\ {D_{3} } \end{array}\right]=\left[\begin{array}{cccccc} {0} & {0} & {0} & {0} & {12.7} & {0} \\ {0} & {0} & {0} & {12.7} & {0} & {0} \\ {-5.2} & {-5.2} & {15.1} & {0} & {0} & {0} \end{array}\right]\frac{{\rm C}}{{\rm m}^{{\rm 2}} } \otimes \] \[\left[\begin{array}{c} {T_{1} } \\ {T_{2} } \\ {T_{3} } \\ {T_{4} } \\ {T_{5} } \\ {T_{6} } \end{array}\right]+\left[\begin{array}{ccc} {13.05} & {0} & {0} \\ {0} & {13.05} & {0} \\ {0} & {0} & {11.5} \end{array}\right]\frac{{\rm nF}}{{\rm m}} \otimes \left[\begin{array}{c} {E_{1} } \\ {E_{2} } \\ {E_{3} } \end{array}\right]\]As shown in the following figure, we here simplify the problem into a 2D problem, in which the plate is simplified into a simply-supported beam with a length of 0.1 m and a thickness of 0.005 m.
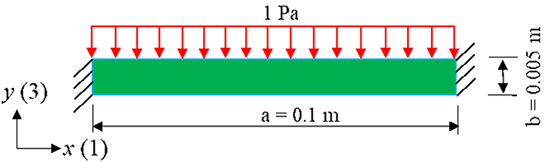
Please predict the distribution of the electric potential with height (thickness) along the vertical axis of the beam (center) generated by a downward vertical distributed load of 1 Pa on the top of the beam.