Hydraulic Field
Theory
$\space$Groundwater Flow
In the real world, water moves in both saturated and unsaturated zones which may coexist as contagious saturated and unsaturated zones, whose boundary may change over time. So, the numerical simulation of such a case requires the simultaneous implementations of the groundwater flow equation and the Richards equation. A standard formulation of the Richards equation that also includes groundwater (saturated zone) flow [Richards, 1931] is \[\frac{S_{{\rm s}} \theta \left(h\right)}{\phi } \frac{\partial h}{\partial t} +\frac{\partial \theta }{\partial t} =\nabla \cdot \left[K_{s} K_{r} \nabla \left(h+z\right)\right]+q_{{\rm H}} ,\] where $h$ is the pressure head, $z$ is the vertical coordinate, $K_{s} $ is the saturated hydraulic conductivity tensor, $K_{r} $is the relative hydraulic conductivity, $S_{{\rm s}} $ is the specific storage coefficient, and $\phi $ is the porosity. The detailed implementation of the equation will be practiced in a later practice problem.
$\space$Surface Flow
The mathematical description of the surface flow resembles that of the flow in porous materials. Mass conservation for surface flow is \[\frac{\partial h}{\partial t} =\nabla \cdot \left(vh\right)+q_{e} +q_{r} , \] where $q_{e} $ is the exchange flux between surface and subsurface domains, and $q_{r} $ is a general source/sink term. Manning's equation is often used to establish a flow depth-discharge relationship, where the velocity vector $v$ in may be written as follows: \[v=\frac{\sqrt{S_{f} } }{n} h^{\frac{2} {3}} , \] where $S_{f} $ [L] is the friction slope and $n$ [TL${}^{-1/3}$] is Manning's coefficient. Other approaches are available to take the place of Manning's equation [Nepf, 1999].
$\space$Example
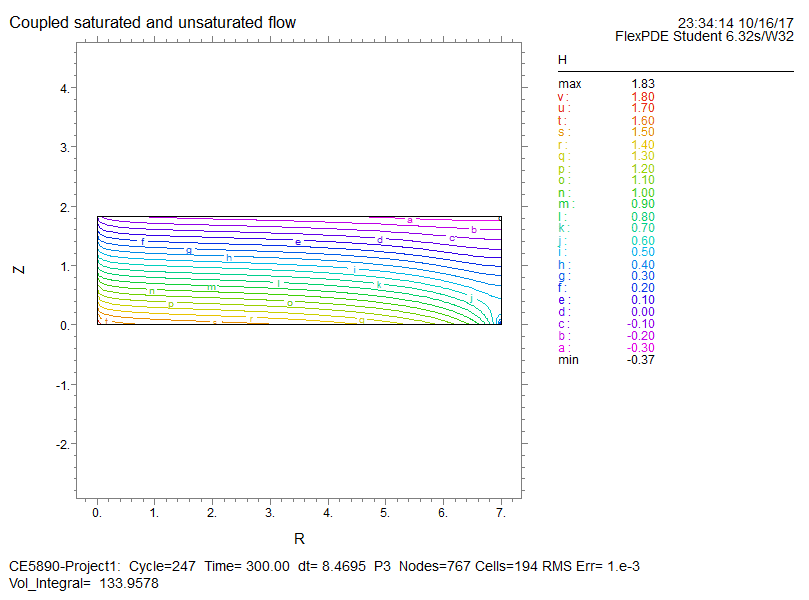
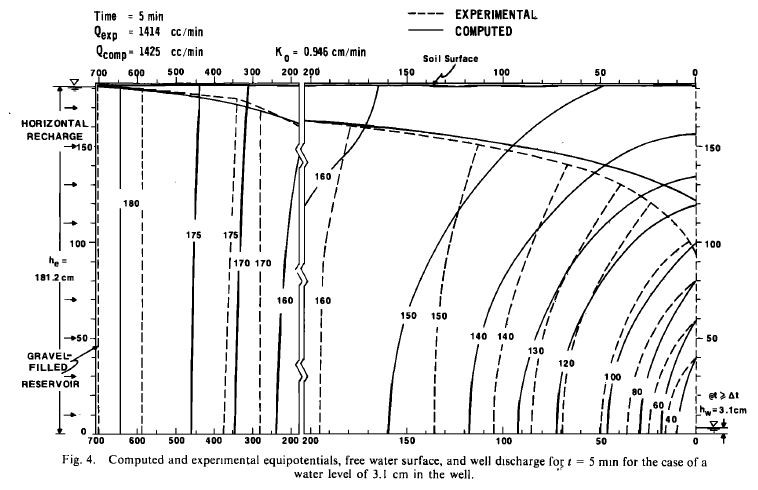
A lab test for mixed saturated-unsaturated flow was conducted and documented by Luthin and Orhun [1975]. The Following figure shows the schematic of a tank used in their test.
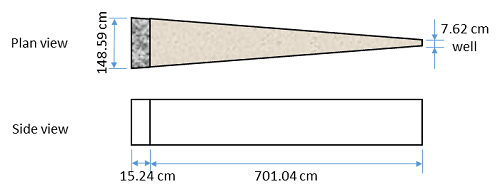
Initially, the sector tank was filled with the sand. A gravel-filled reservoir was placed at the wide end of the tank to simulate a constant horizontal replenishment. Please simulate the experiment and validate your simulation against the lab test.